Les estimations provinciales et territoriales du produit intérieur brut (PIB) réel par industrie reposent sur la formule de l'indice en chaîne de FisherNote 1, et elles ne sont pas additives. La non-additivité des séries réelles provient à la fois de l'enchaînement et de la formule de Fisher elle-même. L'enchaînement détruit la cohérence additive des équations comptables, et la formule de Fisher n'est pas dotée de la propriété d'additivité. Étant donné que les agrégats réels ne sont pas additifs, il est plus difficile de mesurer la contribution d'un agrégat, d'un secteur ou d'une industrie à l'économie totale, car la somme des composantes sous-jacentes n'équivaut pas au total. Ce problème d'additivité s'accroît à mesure que l'on s'éloigne de l'année de référence et que les prix relatifs changent.
Il y a diverses façons de surmonter ce problème d'additivité. Pour une analyse des parts des industries ou des provinces ou territoires, les valeurs courantes (ou prix courants) peuvent représenter une solution suffisante ou même souhaitable, car elles reflètent la structure de l'économie aux prix de la période examinée. Cependant, pour une analyse de la croissance, les valeurs courantes ne sont pas toujours indiquées, car elles combinent à la fois les variations de prix et de volumes. Par exemple, l'augmentation (ou la diminution) de la valeur nominale d'une industrie dans une province ou un territoire donné pourrait y être le résultat de combinaisons diverses de variations de prix et de volume (figure 1) au sein de l'économie, ce qui aura également une incidence sur la contribution de cette industrie aux variations nominales nationales.
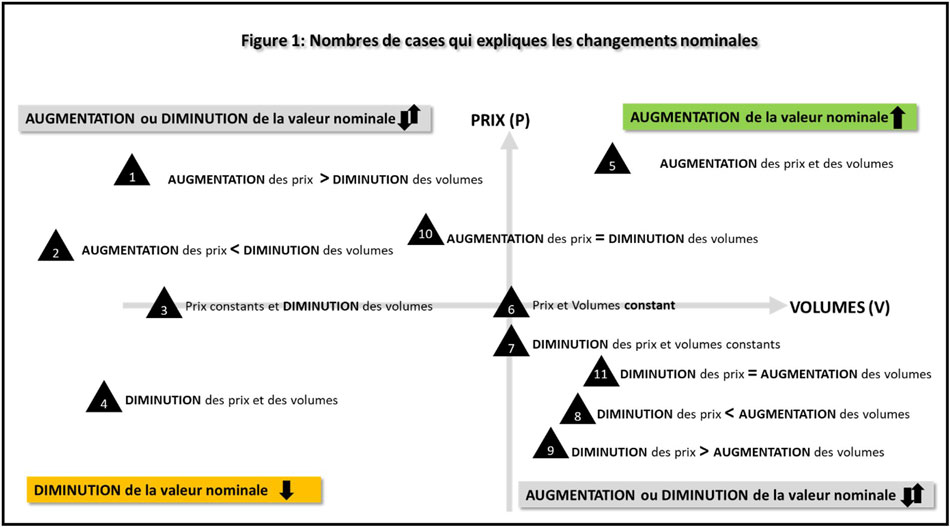
Description de la figure 1
Le titre de la figure 1 est « Nombre de cas pouvant expliquer les variations nominales ».
La figure 1 montre le nombre de mouvements possibles des prix et des volumes qui peuvent se produire dans l'économie d'une période à l'autre pour divers biens et services pour les variations nominales.
- L'augmentation des prix peut être supérieure à la diminution du volume.
- L'augmentation des prix peut être inférieure à la diminution du volume.
- Le prix peut rester inchangé alors que le volume diminue.
- Le prix et les volumes peuvent tous deux diminuer.
- Le prix et les volumes peuvent tous deux augmenter.
- Le prix et les volumes peuvent tous deux rester inchangés.
- Le prix peut diminuer alors que les volumes restent inchangés.
- La baisse du prix peut être inférieure à l'augmentation des volumes.
- La baisse du prix peut être supérieure à l'augmentation des volumes.
- L'augmentation du prix est identique à la diminution du volume.
- La diminution du prix est identique à l'augmentation du volume.
Comme le montre la figure 1, il devient difficile en raison des combinaisons différentes de prix et de volume de déterminer si une variation nominale est attribuable à une variation de prix ou de volume ou à une combinaison des deux. Les estimations du produit intérieur brut (PIB) fondées sur la formule de Fisher sont ajustées pour tenir compte des fluctuations de prix de façon à pouvoir analyser les mouvements de volume « réels ». Comme nous l'avons vu plus haut, puisque les estimations fondées sur la formule de Fisher ne sont pas additives, il peut être difficile d'analyser la façon dont les industries des provinces ou des territoires contribuent à leur propre économie totale et, par la suite, la façon dont les provinces et les territoires contribuent à la croissance réelle de l'économie canadienne.
Les formules de la contribution à la variation en pourcentage (CVP) et de la contribution à la variation nationale en pourcentage (CVNP), qui présentent une décomposition strictement additive de la variation des agrégats, fournissent une mesure complémentaire utile. Les formules repondèrent la contribution des séries détaillées de telle sorte qu'elles deviennent strictement additives à la variation totale de l'agrégat.
La formule de la CVP est une fonction du PIB en valeurs courantes, des volumes du PIB selon le Paasche et le Laspeyres et de l'indice de volume de Fisher.
CVP
où
PIBCi: est le PIB en valeurs courantes pour l'industrie i aux temps t et t-1
PIBLi: est le volume du PIB de Laspeyres pour l'industrie i au temps t
PIBPi: est le volume du PIB de Paasche pour l'industrie i au temps t-1
FV: est l'indice de volume de Fisher au temps t
Cette formule constitue le fondement de la série sur la CVP publiée par le programme du PIB provincial et territorial par industrie.Elle permet de mesurer la contribution d'une industrie ou d'un agrégat à la variation en pourcentage du PIB total en termes « réels ».
Le tableau 1 donne un exemple de contribution à la variation en pourcentage dans le contexte d'un indice de Fisher. Tel que souligné ci-dessus, la somme des industries détaillées n'équivaut pas à l'indice total pour les colonnes t et t-1, ce qui fait qu'il est difficile d'établir un rapport entre les taux de croissance de chacune des industries et le taux de croissance de l'agrégat. La CVP, cependant, fournit une mesure complètement additive de la contribution de chaque industrie au taux de croissance de l'agrégat.
| Industrie | t-1 | t | Taux de croissance | CVP |
|---|---|---|---|---|
| A | 108 | 144 | 33,33 % | 1,98 |
| B | 224 | 238 | 6,25 % | 1,66 |
| C | 525 | 540 | 2,86 % | 1,49 |
| D | 150 | 162 | 8,00 % | 1,22 |
| Total (Fisher) | 1003,7 | 1067,4 | 6,35 % | 6,35 |
Bien que la mesure de la CVP examinée ci-dessus soit utile pour analyser comment les industries ou un agrégat contribuent à l'économie de leur propre province ou territoire, elle ne montre pas comment une industrie ou un agrégat au sein d'une province ou d'un territoire contribue à la croissance réelle de l'économie nationale. La formule de la CVNP permet de mesurer la contribution d'une industrie ou d'un agrégat d'une province ou d'un territoire à la variation en pourcentage du PIB national total en termes « réels ».
CVNP
Où
PIBCi,j: est le PIB en valeurs courantes pour l'industrie i et pour la province ou le territoire j aux temps t et t-1
PIBLi,j: est le volume du PIB de Laspeyres pour l'industrie i et pour la province ou le territoire j au temps t
PIBPi,j: est le volume du PIB de Paasche pour l'industrie i et pour la province ou le territoire j au temps t-1
FVN: est l'indice de volume nationale de Fisher au temps t
Le tableau 2 donne des exemples de contribution provinciale et territoriale à la variation en pourcentage au Canada dans le contexte d'un indice de Fisher. Comme pour le tableau 1, la somme des provinces et des territoires selon l'industrie n'y équivaut pas à l'indice total pour les colonnes t et t-1, ce qui fait qu'il est difficile d'établir un rapport entre les taux de croissance de l'économie des provinces et des territoires selon l'industrie et le taux de croissance de l'économie nationale. La CVNP, cependant, fournit une mesure complètement additive de la contribution de chaque industrie d'une province ou d'un territoire au taux de croissance total de l'économie du pays.
| Région géographique | Industrie | t-1 | t | Taux de croissance | CVNP |
|---|---|---|---|---|---|
| Géo 1 | A | 102 767 | 109 633 | 6,68 % | 0,35 |
| B | 1 099 806 | 1 123 901 | 2,19 % | 1,25 | |
| Géo 2 | A | 711 388 | 731 888 | 2,88 % | 1,07 |
| B | 10 335 | 11 842 | 14,58 % | 0,08 | |
| Total national | Total (Fisher) | 1 926 783 | 1 979 750 | 2,75 % | 2,75 |
Bien que la comparaison des statistiques de différentes périodes soit une application acceptable de la mesure de la CVP et de la CVNP, elle ne devrait pas être utilisée pour mener une analyse du taux de croissance d'une période à l'autre. De plus, la contribution à la variation en pourcentage ne doit pas être interprétée comme une proportion.