Privacy preserving technologies, part three: Private statistical analysis and private text classification based on homomorphic encryption

By: Benjamin Santos and Zachary Zanussi, Statistics Canada

Introduction

What's possible in the realm of the encrypted and what use cases can be captured with homomorphic encryption? The Data Science Network's first article in the privacy preserving series, A Brief Survey of Privacy Preserving Technologies, introduces privacy enhancing technologies^{Footnote 1} (PETs) and how they enable analytics while protecting data privacy. The second article in the series, Privacy Preserving Technologies Part Two: Introduction to Homomorphic Encryption, took a deeper look at one of the PETs, more specifically homomorphic encryption (HE). In this article, we describe applications explored by data scientists at Statistics Canada in encrypted computation.

HE is an encryption technique that allows computation on encrypted data as well as several paradigms for secure computing. This technique includes secure outsourced computing, where a data holder allows a third party (perhaps, the cloud) to compute on sensitive data while ensuring that input data is protected. Indeed, if the data holder wants the cloud to compute some (polynomial) function $f$ on their data $v$ , they can encrypt it into a ciphertext, denoted $[v]$ , send it safely to the cloud which computes $f$ homomorphically to obtain $[f (v)]$ , and forward the result back to the data holder, who can decrypt and view $f (v)$ . The cloud has no access to the input, output, or any intermediate data values.

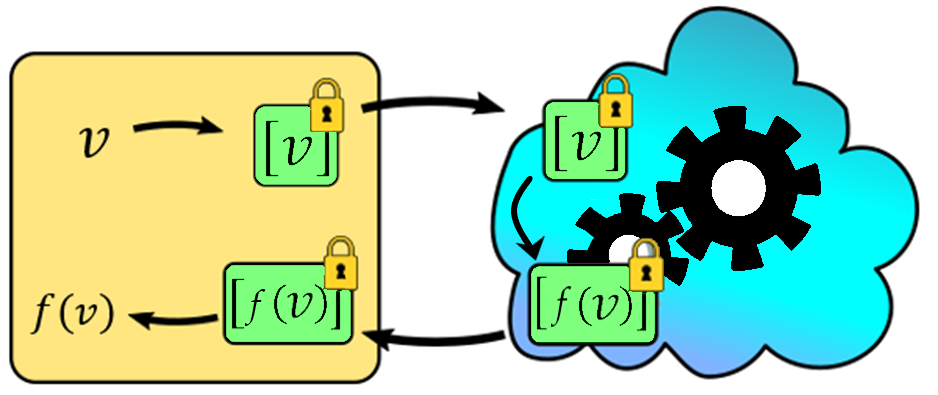
Figure 1: Illustration of a typical HE workflow.

An illustration of a typical HE workflow. The data, $v$ , is encrypted, putting it in a locked box $[v]$ . This value is sent to the compute party (the cloud). Gears turn and the input encryption $[v]$ is transformed into the output encryption, $[f (v)]$ , as desired. This result is forwarded back to the owner who can take it out of the locked box and view it. The cloud doesn't have access to input, output, or intermediate values.

HE is currently being considered by international groups for standardization. The Government of Canada does not recommend HE or the use of any cryptographic technique before it's standardized. While HE is not yet ready for use on sensitive data, this is a good time to explore its capabilities and potential use cases.

Scanner data

Statistics Canada collects real time data from major retailers for a variety of data products. This data describes the daily transactions performed such as a description of the product sold, the transaction price, and metadata about the retailer. This data is called "scanner data", after the price scanners used to ring a customer through checkout. One use of scanner data is to increase the accuracy of the Consumer Price Index, which measures inflation and the strength of the Canadian dollar. This valuable data source is treated as sensitive data—we respect the privacy of the data and the retailers that provide it.

The first step in processing this data is to classify the product descriptions into an internationally standardized system of product codes known as the North American Product Classification System (NAPCS) Canada 2017 Version 1.0. This hierarchical system of seven-digit codes is used to classify different types of products for analysis. For example, one code may correspond to coffee and related products. Each entry in the scanner data needs to be assigned one of these codes based on the product description given by the retailer. These descriptions, however, are not standardized and may differ widely between different retailers or across different brands of similar products. Thus, the desired task is to convert these product descriptions, which often include abbreviations and acronyms, into their codes.

After they've been classified, the data is grouped based on its NAPCS code and statistics are computed on these groups. This allows us to gain a sense of how much is spent on each type of product across the country, and how this value changes over time.

Figure 2: High level overview of the scanner data workflow with sample data.

High level overview of the scanner data workflow. First, the product descriptions are classified into NAPCS codes. Examples are given: "mochi ice cream bon bons" is assigned NAPCS code 5611121, while "chipotle barbeque sauce" is assigned 5611132. Application 2 is to assign these codes to the descriptions. The product descriptions have a few identifiers and a price value attached. Application 1 is to sort the data by these codes and identifiers, and compute statistics on the price values.

Sample dataset 1

Description ID1 ID2 Value

"mochi ice cream bon bons" 054 78 $5.31

"chipotle barbeque sauce" 201 34 $3.80

Application 2

Sample dataset 2

NAPCS ID1 ID2 Value

5611121 054 78 $5.31

5611132 201 34 $3.80

Application 1

Statistics (total, mean, variance)

Sample dataset 1
Description	ID1	ID2	Value
"mochi ice cream bon bons"	054	78	$5.31
"chipotle barbeque sauce"	201	34	$3.80

Sample dataset 2
NAPCS	ID1	ID2	Value
5611121	054	78	$5.31
5611132	201	34	$3.80

Given the data's sensitivity and importance, we've targeted it as a potential area where PETs can preserve our data workflow while maintaining the high level of security required. The two tasks above have, up to now, been performed within Statistics Canada's secure infrastructure, where we can be sure the data is safe at the time of ingestion and throughout its use. In 2019, when we were first investigating PETs within the agency, we decided to experiment using the cloud as a third-party compute resource, secured by HE.

We model the cloud as a semi-honest party, meaning it will follow the protocol we assign it, but it will try to infer whatever it can about the data during the process. This means we need sensitive data to always be encrypted or obscured. As a proof-of-concept, we replaced the scanner data with a synthetic data source, which allows us to conduct experiments without putting the security of the data at risk.

Application 1: Private statistical analysis

Our first task was to perform the latter part of the scanner data workflow – the statistical analysis. We constructed a synthetic version of the scanner data to ensure its privacy. This mock scanner data consisted of thirteen million records, each consisting of a NAPCS code, a transaction price, and some identifiers. This represents about a week's worth of scanner data from a single retailer. The task was to sort the data into lists, encrypt it, forward it to the cloud, and instruct the cloud to compute the statistics. The cloud would then forward us the still-encrypted results, so we could decrypt and use them for further analysis.

Suppose our dataset is sorted into lists of the form $v = (v_{1}, \dots, v_{l})$ . It's relatively straightforward to encrypt each value $v_{i}$ into a ciphertext $[v_{i}]$ and send the list of ciphertexts $([v_{1}], \dots, [v_{l}])$ to the cloud. The cloud can use homomorphic addition and multiplication to calculate the total, mean, and variance and return these as ciphertexts to us (we'll see how division is handled for the mean and variance later in this article). We do this for every list, and decrypt and view our data. Simple, right?

The problem with a naïve implementation of this protocol is data expansion. A single CKKS^{Footnote 2} ciphertext is a pair of polynomials of degree $2^{14}$ with 240-bit coefficients. All together, it may take 1 MB to store a single record. Over the entire dataset of thirteen million, this becomes 13 TB of data! The solution to this problem is called packing.

Packing

Ciphertexts are big, and we have a many small pieces of data. We can use packing to store an entire list of values into a single ciphertext, and the CKKS scheme allows us to perform Single Instruction Multiple Data (SIMD) type operations on that ciphertext, so we can compute several statistics at once! This ends up being a massive increase in efficiency for many HE tasks, and a clever data packing structure can make the difference between an intractable problem and a practical solution.

Suppose we have a list of $l$ values, $v = (v_{1}, v_{2}, \dots, v_{l})$ . Using CKKS packing, we can pack this entire list into a single ciphertext, denoted by $[v]$ . Now, the operations of homomorphic addition and multiplication occur slot-wise in a SIMD fashion. That is, if $u = (u_{1}, u_{2}, \dots, u_{l})$ encrypts to $[u]$ , then we can compute homomorphic addition to get

$[u] \oplus [v] = [u + v]$

where $[u + v]$ is an^{Footnote 3} encryption of the list $(u_{1} + v_{1}, u_{2} + v_{2}, \dots, u_{l} + v_{l})$ . This homomorphic addition takes as much time to compute as if there was only one value in each ciphertext, so it's clear we can get an appreciable efficiency boost via packing. The downside is that we now must use this vector structure in all of our calculations, but with a little effort, we can figure out how to vectorize relevant calculations to take advantage of packing.

Figure 3: An illustration of packing. The four values can either be encrypted into four separate ciphertexts, or all be packed into one.

An illustration of packing. Four values, $v_{1}, v_{2}, v_{3}, v_{4}$ , need to be encrypted. In one case, they can all be encrypted into separate ciphertexts, depicted as locked boxes. In another, we can pack all four values into a single box. In the former case, it will take four boxes, which is less efficient to store and to work with. The latter case, packing as many values as possible, is almost always preferred.

Now I know what you are thinking - doesn't packing, which stores a bunch of values within a vector, make it impossible to compute values within a list? That is, if we have $v = (v_{1}, v_{2}, \dots, v_{l})$ , what if I wanted $v_{1} + v_{2}$ ? We have access to an operation known as rotation. Rotation takes a ciphertext that is an encryption of $(v_{1}, v_{2}, \dots, v_{l})$ and turns it into $R o t ([v])$ , which is an encryption of $(v_{2}, v_{3}, \dots, v_{l}, v_{1})$ . That is, it shifts all the values left in one slot, sliding the first value into the last slot. So, by computing $[v] \oplus R o t ([v])$ , we get

$(v_{1} + v_{2}, v_{2} + v_{3}, \dots, v_{l} + v_{1})$ ,

and the desired value is in the first slot.

Mathematically, packing is achieved by exploiting the properties of the cleartext, plaintext and ciphertext spaces. Recall that the encryption and decryption functions are maps between the latter two spaces. Packing requires another step called encoding, which encodes a vector of (potentially complex, though in our case, real) values $v$ from the cleartext space into a plaintext polynomial $p$ . While the data within $p$ is not human-readable as-is, it can be decoded into the vector of values by any computer without requiring any keys. The plaintext polynomial $p$ can then be encrypted into the ciphertext $[v]$ and used to compute statistics on scanner data.^{Footnote 4}

Efficient statistical analysis using packing

Getting back to the statistical analysis on scanner data, remember that the problem was that encrypting every value into a ciphertext was too expensive. Packing will allow us to vectorize this process, making its orders of magnitude more efficient in terms of communication and computation.

We can now begin to compute the desired statistics on our list $v = (v_{1}, v_{2}, \dots, v_{l})$ . The first value of interest is the total, $T_{v} = \sum_{i = 1}^{l} v_{i}$ , obtained by summing all the values in the list. After encrypting $v$ into a packed ciphertext $[v]$ , we can simply add rotations of the ciphertext $[v]$ to itself until we have a slot with the sum of all the values. In fact, we can do better than this naïve strategy of $l$ rotations and additions- we can do it in $\log_{2} l$ steps by rotating one slot first, then by two slots, then four, then eight, and so on until we get the total $T_{v}$ in a slot.

Next, we want the mean, $M_{v} = T_{v} / l$ . To do this, we encrypt the value $1 / l$ into the ciphertext $[1 / l]$ and send it along with the list $[v]$ . We can then simply multiply this value by the ciphertext that we got when computing the total. It's a similar story for the variance, $V_{v} = 1 / l \sum_{i = 1}^{l} (v_{i} - M_{v})^{2}$ , where we subtract the mean from $[v]$ , multiply the result by itself, compute the total again, and then multiply again by the $[1 / l]$ ciphertext.

Let's investigate the savings that packing afforded us. In our case, we had about 13 million data points which separates into 18,000 lists. Assuming that we could pack every list into a single ciphertext, that reduces the size of the encrypted dataset by almost three orders of magnitude. But in reality, the different lists were all different sizes, with some being as large as tens of thousands of entries and others as small as two or three, with the majority falling in the range of hundreds to thousands. Through some clever manipulation, we were able to pack multiple lists into single ciphertexts and run the total, mean, and variance algorithms for them all at once. By using ciphertexts that can pack 8,192 values at once, we were able to reduce the number of ciphertexts to just 2,124. At about 1 MB per ciphertext, this makes the encrypted dataset about two gigabytes (GBs). With the cleartext data taking 84 megabytes (MB), this left us with a data expansion factor of about 25 times. Overall, the encrypted computation took around 19 minutes, which is 30 times longer than unencrypted.

Application 2: Private text classification based on homomorphic encryption

Next, we tackled the machine learning training task. Machine learning training is a notoriously expensive task, so it was unclear whether we'd be able to implement a practical solution.

Next, we tackled the machine learning training task. Machine learning training is a notoriously expensive task, so it was unclear whether we'd be able to implement a practical solution. Recall the first task in the scanner data workflow - the noisy, retailer-dependent product descriptions need to be classified into the NAPCS codes. This is a multiclass text classification task. We created a synthetic dataset from an online repository of product descriptions and tagged them with one of five NAPCS codes.

Running a neural network is basically multiplying a vector past a series of matrices, and training a neural network involves forward passes, which is evaluating training data in the network, as well as backward passes, which is using (stochastic) gradient descent and the chain rule to find the best way to update the model parameters to improve performance. All this boils down to multiplying values by other values, and by having access to homomorphic multiplication, training an encrypted network is possible in theory. In practice, this is hampered by a core limitation of the CKKS scheme: the leveled nature of homomorphic multiplications. We'll discuss this element first, and then explore the different protocol aspects designed to mitigate it.

Ciphertext levels in CKKS

In order to protect your data during encryption, the CKKS scheme adds a small amount of noise to each ciphertext. The downside is that this noise accumulates with consecutive operations and needs to be modulated. CKKS has a built-in mechanism for this, but unfortunately it only allows for a bounded number of operations on a single ciphertext.

Suppose we have two freshly encrypted ciphertexts - $[v_{1}]$ and $[v_{2}]$ . We can homomorphically multiply them to get the ciphertext $[v_{1} \otimes v_{2}]$ . The problem is that the noise^{Footnote 5} in this resulting ciphertext is much larger than in the freshly encrypted ones, so if we multiplied it by freshly encrypted $[v_{3}]$ , the result would be affected by this mismatch.

What would first have to rescale the ciphertext $[v_{1} \otimes v_{2}]$ . This is transparently handled by the HE library, but under the hood, the ciphertext is moved to a slightly different space. We say that $[v_{1} \otimes v_{2}]$ has been moved down a level, meaning. the ciphertext started out on level $L - 1$ , and after rescaling, it is left on level $L - 1$ . The value $L$ is determined by the security parameters we chose when we set up the HE scheme.

Now we have $[v_{1} \otimes v_{2}]$ which has a normal amount of noise but is on level $L - 1$ , and the freshly encrypted $[v_{3}]$ which is still on level $L$ . Unfortunately, we can't perform operations on ciphertexts that are on different levels, so we first have to reduce the level of $[v_{3}]$ to $L - 1$ by modulus switching. Now that both ciphertexts are on the same level, we can finally multiply them as desired. We don't need to rescale the result of additions, but we do for every multiplication.

Figure 4: An illustration of levels

An illustration of levels. On the left we can see the level on which each ciphertext resides: from top to bottom, we have levels $L$ , $L - 1$ , and $L - 2$ . Freshly encrypted $v_{1}$ , $v_{2}$ , and $v_{3}$ all inhabit level $L$ on top. After multiplying, $v_{1} \otimes v_{2}$ move down to level $L - 1$ . If we want to multiply $v_{1} \otimes v_{2}$ by $v_{3}$ , we need to first bring $v_{3}$ down to level $L - 1$ . The resulting product, $v_{1} \otimes v_{2} \otimes v_{3}$ lives on level $L - 2$ .

This leveled business has two consequences. One, the developer needs to be conscious of the level of the ciphertexts they're using. And two, the ciphertexts will eventually reach level 0 after many consecutive multiplications, at which point it's spent, and we can't perform any more multiplications.

There are a few options for extending computations beyond the number of levels available. The first is a process called bootstrapping, where the ciphertext is homomorphically decrypted and re-encrypted, resulting in a fresh ciphertext. This process can theoretically result in an unbounded number of multiplications. However, the added expense adds a cost to the computation. Alternatively, one can refresh the ciphertexts by returning them to the secret key holder, who can decrypt and re-encrypt them before returning them to the cloud. Sending ciphertexts back and forth adds a communication cost but this is sometimes worth it when there aren't many ciphertexts to send.

Impact of levels on our network structure

We had to consider this fundamental constraint on HE when designing our neural network. The process of training a network involves performing a prediction, evaluating the prediction, and updating the model parameters. This means that every round, or epoch, of training consumes multiplicative levels. We tried to minimize the number of multiplications needed to traverse forward and backward through the network to maximize the number of training rounds available. We'll now describe the network structure and the data encoding strategy.

The network architecture was inspired by the existing solution in production. This amounted to an ensemble model of linear learners. We trained several single layer networks separately, and at prediction time, we had each learner vote on each entry. We chose this approach because it reduced the amount of work required to train each model - less training time meant fewer multiplications.

Each layer in a neural network is a weight matrix of parameters multiplied by data vectors during the forward pass. We can adapt this to HE by encrypting each input vector into a single ciphertext and encrypting each row of the weight matrix into another ciphertext. The forward pass then becomes several vector multiplications, followed by logarithmically many rotations and multiplications to compute the sum of the outputs (recall that matrix multiplication is a series of dot products, which are a component-wise multiplication followed by computing the sum resulting values).

Preprocessing is an important part of any text classification task. Our data were short sentences which often contained acronyms or abbreviations. We chose to use a character $n$ -gram encoding with $n$ equal to three, four, five, and six - "ice cream" was broken into the 3-grams {"ice", "cre", "rea", "eam"}. These $n$ -grams were collected and enumerated over the entire dataset and were used to one-hot encode each entry. A hashing vectorizer^{Footnote 6} was used to reduce the dimension of the encoded entries.

Similarly, to how we packed multiple lists together in the statistical analysis, we found we could pack together multiple models and train them at once. Using a value $N = 2^{15}$ meant we could pack 16,384 values into each ciphertext, so if we hashed our data to 4,096 dimensions, we could fit four models into each ciphertext. This had the added benefit of reducing the number of ciphertexts required to encrypt our dataset by a factor of four. Meaning we could train four models simultaneously.

Our choice of encryption parameters meant we had between 12 and 16 multiplications before we ran out of levels. With a single layer network, the forward pass and backward pass took two multiplications each, leaving us room for three to four epochs before our model ciphertexts were spent. Our ensembles meant we could train several ciphertexts worth of models if desired, meaning we could have as many learners as desired at the cost of additional training time. Carefully modulating which models learned on what data helped us maximize the overall performance of the ensemble.

Our dataset consisted of 40,000 training examples and 10,000 test examples each evenly distributed over our five classes. To train four submodels for six epochs took five hours and resulted in a model that obtained 74% accuracy on the test set. Using the ciphertext refreshing tactic previously described, we can hypothetically train for as many epochs as we'd like, though every refresh adds more communication cost to the process^{Footnote 7}. After training, the cloud sends the encrypted model back to StatCan, and we can run it in the cleartext on data in production. Or we can keep the encrypted model on the cloud and run encrypted model inference when we have new data to classify.

Conclusion

This concludes the Statistics Canada series of applications of HE to scanner data explored to date. HE has a number of other applications which might prove interesting to a national statistics organization such as Private Set Intersection, in which two or more parties jointly compute the intersection of private datasets without sharing them, as well as Privacy Preserving Record Linkage, where parties additionally link, share, and compute on microdata attached to their private datasets.

There's a lot left to explore in the field of PETs and StatCan is working to leverage this new field to protect the privacy of Canadians while still delivering quality information that matters.

Meet the Data Scientist

If you have any questions about my article or would like to discuss this further, I invite you to Meet the Data Scientist, an event where authors meet the readers, present their topic and discuss their findings.

Thursday, December 15
2:00 to 3:00 p.m. ET
MS Teams – link will be provided to the registrants by email

Register for the Data Science Network's Meet the Data Scientist Presentation. We hope to see you there!

Footnotes

Footnote 1

The terminology "privacy enhancing techniques (PPT)" was used in previous articles of the series. However, the term "privacy enhancing technologies (PET)" is also used interchangeably within the literature.

Return to footnote 1 referrer

Footnote 2

Named after the authors Cheon, Kim, Kim, & Song of a homomorphic encryption scheme for arithmetic of approximate numbers, see references.

Return to footnote 2 referrer

Footnote 3

This is a subtle but important point to make. The encryption function employed in homomorphic encryption is always randomized, so that computing the encryption of the same value with the same key twice gives you different encryptions. This is necessary, because otherwise an adversary can simply compute encryptions of a bunch of different values and try to match them against unknown encrypted data. This requirement is known as semantic security in the cryptographic community.

Return to footnote 3 referrer

Footnote 4

A more detailed explanation is given here: CKKS explained: Part 1, Vanilla Encoding and Decoding

Return to footnote 4 referrer

Footnote 5

There are two factors at play here. Not only is the noise larger in the product ciphertext, but the scale is also larger. We won't discuss scale in this article, but the interested reader can learn more here: Craig Gentry's PhD Thesis.

Return to footnote 5 referrer

Footnote 6

A hashing vectorizer is a technique used in Natural Language Processing that converts a collection of text documents to a matrix of token occurrences. A popular implementation can be found here: sklearn.feature_extraction.text.HashingVectorizer

Return to footnote 6 referrer

Footnote 7

To put things in perspective, the cleartext model attains nearly the same accuracy in 80 epochs on a few seconds of overall training time.

Return to footnote 7 referrer

References

North American Product Classification System (NAPCS) Canada 2017 Version 1.0

Cheon, J. H., Kim, A., Kim, M., & Song, Y. (2016). Homomorphic Encryption for Arithmetic of Approximate Numbers.Cryptology ePrint Archive.

C. Gentry. (2009). A fully homomorphic encryption scheme. PhD thesis, Stanford University: Craig Gentry's PhD Thesis

Zanussi, Z., Santos B., & Molladavoudi S. (2021). Supervised Text Classification with Leveled Homomorphic Encryption. In Proceedings 63rd ISI World Statistics Congress (Vol. 11, p. 16). International Statistical Institute - Statistical Science for a Better World

Report a problem or mistake on this page

Date modified:: 2022-12-05

Language selection

WxT Language switcher

Search and menus

WxT Search form