Technologies liées à la protection de la vie privée, partie trois : Analyse statistique confidentielle et classification de texte confidentiel fondées sur le chiffrement homomorphe
Par : Benjamin Santos et Zachary Zanussi, Statistique Canada
Introduction
Qu'est-ce qui est possible dans le domaine du chiffrement et quels cas d'utilisation peuvent être visés par le chiffrement homomorphe? Le premier article du Réseau de la science des données dans la série sur la protection de la vie privée, Une brève enquête sur les technologies liées à la protection de la vie privée, présente les technologies d'amélioration de la confidentialitéNote de bas de page 1 (TAC) et la façon dont elles permettent l'analyse tout en protégeant la confidentialité des données. Le deuxième article de la série, Technologies liées à la protection de la vie privéepartie deux : introduction au chiffrement homomorphe, a abordé plus en profondeur une des TAC, plus précisément le chiffrement homomorphe (CH). Dans cet article, nous décrivons les applications étudiées par les scientifiques des données de Statistique Canada en matière de traitement informatique à partir de données chiffrées.
Le CH est une technique de chiffrement qui permet d'effectuer des traitements informatiques à partir de données chiffrées ainsi que plusieurs paradigmes pour les traitements informatiques sécurisés. Cette technique comprend le traitement informatique sécurisé à l'externe, selon lequel un détenteur de données permet à un tiers (peut-être le nuage) d'effectuer des traitements informatiques à partir de données de nature délicate, tout en s'assurant que les données d'entrée sont protégées. En effet, si le détenteur de données veut que le nuage calcule une fonction (polynomiale) à partir de ses données , il peut les chiffrer sous forme de cryptogrammes, désignés , les envoyer de façon sécuritaire sur le nuage qui calcule de façon homomorphe pour obtenir et renvoie les résultats au détenteur de données, qui peut déchiffrer et visualiser . Le nuage n'a aucun accès aux valeurs des données d'entrée, de sortie ou intermédiaires.
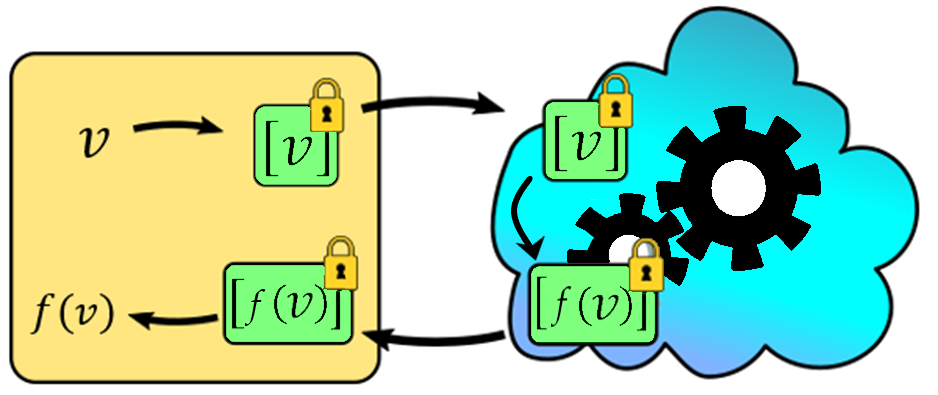
Figure 1 : Illustration d'un flux de travail typique du CH.
Une illustration d'un flux de travail typique du CH. Les données,, sont chiffrées, donc elles sont placées dans une boîte verrouillée . Cette valeur est envoyée au tiers qui effectuera le traitement informatique (le nuage). Les engrenages tournent et le chiffrement d'entrée se transforme en chiffrement de sortie, , comme souhaité. Ce résultat est renvoyé au propriétaire, qui peut le sortir de la boîte verrouillée et le visualiser. Le nuage n'a pas accès aux valeurs d'entrées, de sortie ou intermédiaires.
Des groupes internationaux envisagent actuellement la normalisation du CH. Le gouvernement du Canada ne recommande pas le CH ou l'utilisation des techniques cryptographiques avant que ce soit normalisé. Même si le CH n'est pas encore prêt à être utilisé sur des données de nature délicate, c'est un bon moment pour explorer ses capacités ainsi que d'éventuels cas d'utilisation.
Données de lecteurs optiques
Statistique Canada recueille des données en temps réel auprès des grands détaillants sur divers produits d'information. Ces données décrivent les opérations quotidiennes effectuées comme une description du produit vendu, le prix de vente et les métadonnées au sujet du détaillant. Ces données sont appelées « données de lecteurs optiques », d'après les lecteurs optiques utilisés lorsque les clients passent à la caisse. Une des utilisations des données optiques est d'augmenter la précision de l'Indice des prix à la consommation, qui mesure l'inflation et la vigueur du dollar canadien. Cette précieuse source de données est traitée comme des données de nature délicate – nous respectons la confidentialité des données et des détaillants qui les fournissent.
La première étape dans le traitement de ces données consiste à classer les descriptions de produits dans un système classificatoire normalisé de codification à l'échelle internationale, à savoir le Système de classification des produits de l'Amérique du Nord (SCPAN) Canada 2017 version 1.0. Ce système hiérarchique de codes à sept chiffres est utilisé pour classer les différents types de produits aux fins d'analyse. Il y a un code, par exemple, pour le café et ses produits. Chaque entrée de données scanographiques doit recevoir un de ces codes en fonction de la description du produit fournie par le détaillant. Ces descriptions ne sont toutefois pas normalisées et peuvent être très différentes d'un détaillant à l'autre ou d'une marque à l'autre de produits semblables. Ainsi, la tâche souhaitée est la conversion de ces descriptions de produit, qui comprennent souvent des abréviations et des acronymes, en codes correspondants.
Après avoir été classées, les données sont regroupées en fonction de leur code du SCPAN et les statistiques sont calculées à partir de ces groupes. Cela nous permet d'avoir une idée du montant dépensé pour chaque type de produit dans l'ensemble du pays, et de la façon dont cette valeur change au fil du temps.

Figure 2 : Aperçu de haut niveau du flux de travail des données de lecteurs optiques avec des données-échantillons.
Aperçu de haut niveau du flux de travail des données de lecteurs optiques. D'abord, les descriptions de produit sont classées selon les codes du SCPAN. Des exemples sont fournis : « bonbons mochi à la crème glacée » se voit attribuer le code du SCPAN 5611121, alors que « sauce barbecue chipotle » se voit attribuer le code 5611132. L'application 2 consiste à attribuer ces codes aux descriptions. Les descriptions de produits sont liées à quelques identificateurs et à une valeur de prix. L'application 1 consiste à classer les données selon ces codes et identificateurs, et à calculer des statistiques sur les valeurs de prix.
| Description | ID1 | ID2 | Valeur |
|---|---|---|---|
| « bonbons mochi à la crème glacée » | 054 | 78 | 5.31 $ |
| « sauce barbecue chipotle » | 201 | 34 | 3.80 $ |
Application 2
| SCPAN | ID1 | ID2 | Valeur |
|---|---|---|---|
| 5611121 | 054 | 78 | 5.31 $ |
| 5611132 | 201 | 34 | 3.80 $ |
Application 1
Statistics (total, moyenne, variance)
Étant donné l'importance et la nature délicate des données, nous les avons ciblées comme domaine potentiel pour lequel les TAC pourraient préserver notre flux de travail des données tout en maintenant le niveau élevé de sécurité requis. Les deux tâches ci‑dessus ont, jusqu'à maintenant, été effectuées dans l'infrastructure sécurisée de Statistique Canada, où nous pouvons nous assurer que les données sont en sécurité au moment de l'ingestion et tout au long de leur utilisation. En 2019, quand nous avons commencé à étudier les TAC au sein de l'organisme, nous avons décidé de tenter d'utiliser le nuage à titre de ressource tierce de traitement informatique, sécurisé par le CH.
Nous avons créé un modèle infonuagique semblable à un tiers semi-honnête, ce qui signifie qu'il suivra le protocole que nous lui avons attribué, mais il essaiera de déduire tout ce qu'il peut au sujet des données pendant le processus. Cela signifie qu'il faut que les données de nature délicate soient toujours chiffrées ou masquées. Dans notre validation de principe, nous avons remplacé ces données par une source de données synthétiques, ce qui nous permet de procéder à des expériences sans craindre de nuire à la sécurité des données.
Application 1 : Analyse statistique confidentielle
Notre première tâche était de réaliser la dernière partie du flux de travail des données de lecteurs optiques – l'analyse statistique. Nous avons créé une version synthétique des données de lecteurs optiques pour assurer leur confidentialité. Ces données de lecteurs optiques fictives consistaient en 13 millions d'enregistrements, chacun comprenant un code du SCPAN, un prix de transaction et certains identificateurs. Cela représente environ une semaine de données de lecteurs optiques d'un seul détaillant. La tâche consistait à trier les données en listes, à les chiffrer, à les envoyer au nuage et à demander au nuage de calculer les statistiques. Le nuage nous enverrait ensuite les résultats toujours chiffrés, pour que nous puissions les déchiffrer et les utiliser aux fins d'analyse plus approfondie.
Supposons que notre ensemble de données est classé en listes ayant la forme . Il est relativement simple de chiffrer chaque valeur en cryptogramme , puis d'envoyer la liste de cryptogrammes sur le nuage. Le nuage peut utiliser l'addition et la multiplication homomorphes pour calculer le total, la moyenne et la variance et nous retourner ces cryptogrammes (nous verrons de quelle façon la division est gérée pour la moyenne et la variance plus tard dans le présent article). Nous faisons cela pour chaque liste, puis déchiffrons et visualisons nos données. C'est simple, n'est-ce pas?
Le problème avec une mise en œuvre naïve de ce protocole est l'élargissement des données. Un seul cryptogramme CKKSNote de bas de page 2 représente une paire de polynômes de degré avec des coefficients de 240-octets. Ensemble, cela peut prendre 1 Mo pour stocker un seul enregistrement. Pour l'ensemble de données complet de 13 millions, cela devient 13 To de données! La solution à ce problème s'appelle la mise en paquet.
Mise en paquet
Les cryptogrammes sont gros et nous avons beaucoup de petits éléments de données. Nous pouvons utiliser la mise en paquet pour stocker une liste complète de valeurs en un seul cryptogramme, et le procédé CKKS nous permet d'effectuer des opérations de type SIMD (instruction unique, données multiples) sur ce cryptogramme, donc nous pouvons calculer plusieurs statistiques en même temps! Cela représente une augmentation massive de l'efficacité pour de nombreuses tâches de CH, et une structure intelligente de mise en paquet des données peut faire la différence entre un problème insoluble et une solution pratique.
Supposons que nous avons une liste de valeurs , . En utilisant la mise en paquet CKKS, nous pouvons mettre en paquet cette liste entière en un seul cryptogramme, désigné par . Maintenant, les opérations d'addition et de multiplication homomorphes ont lieu par emplacement selon le principe du SIMD, c'est‑à‑dire que, si est chiffré , nous pouvons alors calculer l'addition homomorphe pour obtenir
où est unNote de bas de page 3 chiffrement de la liste . Cette addition homomorphe prend autant de temps à calculer que s'il y avait une seule valeur dans chaque cryptogramme; donc il est évident que nous pouvons obtenir un gain d'efficacité appréciable au moyen de la mise en paquet. L'inconvénient est que nous devons maintenant utiliser cette structure vectorielle dans tous nos calculs, mais avec un peu d'efforts, nous pouvons trouver un moyen de vectoriser les calculs pertinents pour profiter de la mise en paquet.

Figure 3 : Une illustration de la mise en paquet. Les quatre valeurs peuvent soit être chiffrées en quatre cryptogrammes séparés, ou être toutes mises en paquet en un seul cryptogramme.
Une illustration de la mise en paquet. Quatre valeurs, doivent être chiffrées. Dans un cas, elles peuvent toutes être chiffrées en cryptogrammes séparés, illustrés sous forme de boîtes verrouillées. Dans l'autre cas, nous pouvons mettre en paquet les quatre valeurs en une seule boîte. Dans le premier cas, cela prendra quatre boîtes, ce qui est moins efficace pour le stockage et les manipulations. Le dernier cas, la mise en paquet d'autant de valeurs que possible, est presque toujours préférable.
Je sais ce que vous pensez : la mise en paquet, qui stocke une série de valeurs dans un vecteur, ne rend-elle pas impossible le calcul des valeurs dans une liste? C'est-à-dire que, si nous avons , que ce passe-t-il si je voulais ? Nous avons accès à une opération appelée rotation. La rotation prend un cryptogramme qui représente le chiffrement de et le transforme en , qui représente le chiffrement de , c'est‑à‑dire qu'il déplace toutes les valeurs à gauche d'un emplacement, glissant la première valeur dans le dernier emplacement. Donc, en calculant , nous obtenons
et la valeur souhaitée est dans le premier emplacement.
Mathématiquement, la mise en paquet est réalisée en exploitant les propriétés du texte clair, du texte brut et des espaces du texte chiffré. Souvenez-vous que les fonctions de chiffrement et de déchiffrement sont des cartes entre les deux derniers espaces. La mise en paquet exige une autre étape appeléeencodage, qui code un vecteur (potentiellement complexe, mais dans notre cas, réel) de valeurs à partir de l'espace du texte clair en un polynôme de texte brut . Les données de ne sont pas lisibles par un humain, mais elles peuvent être décodées en fonction du vecteur des valeurs par tout ordinateur sans avoir à recourir à des clés. Le polynôme de texte brut peut être chiffré en cryptogramme et utilisé pour calculer les statistiques sur les données de lecteurs optiques.Note de bas de page 4
Analyse statistique efficace au moyen de la mise en paquet
Pour revenir à l'analyse statistique des données de lecteurs optiques, souvenez‑vous que le problème était que le chiffrement de chaque valeur en cryptogramme était trop coûteux. La mise en paquet nous permettra de vectoriser ce processus, rendant ses ordres de grandeur plus efficaces en matière de communication et de calcul.
Nous pouvons maintenant commencer à calculer les statistiques désirées de notre liste . La première valeur d'intérêt est le total,, obtenu en additionnant toutes les valeurs dans la liste. Après avoir chiffré en un cryptogramme mis en paquet , nous pouvons simplement ajouter des rotations du cryptogramme à lui‑même jusqu'à ce que nous ayons un emplacement avec la somme de toutes les valeurs. En fait, nous pouvons faire mieux que cette stratégie naïve de rotations et d'additions – nous pouvons le faire en étapes en faisant d'abord une rotation d'un emplacement, puis de deux, puis de quatre, puis de huit jusqu'à ce que nous obtenions le total dans un emplacement.
Ensuite, nous voulons la moyenne, . Pour faire cela, nous chiffrons la valeur en cryptogramme et l'envoyons avec la liste . Nous pouvons ensuite simplement multiplier cette valeur par le cryptogramme que nous avons obtenu lorsque nous avons calculé le total. Il en va de même pour la variance, , où nous soustrayons la moyenne par , multiplions le résultat par lui-même, calculons de nouveau le total, puis le multiplions de nouveau par le cryptogramme .
Examinons les économies que la mise en paquet nous a permis de faire. Dans notre cas, nous avions environ 13 millions de points de données qui ont été séparés en 18 000 listes. En supposant que nous pourrions mettre en paquet chaque liste en un seul cryptogramme, cela réduit la taille des ensembles de données chiffrées de près de trois ordres de grandeur. Mais en réalité, les différentes listes avaient toutes des tailles différentes, certaines comptant des dizaines de milliers d'entrées et d'autres n'en comptant que deux ou trois, dont la majorité se situait dans la fourchette des centaines aux milliers. Au moyen d'une manipulation intelligente, nous avons été capables de mettre en paquet de multiples listes en cryptogrammes uniques et d'exécuter les algorithmes de total, de moyenne et de variance pour celles‑ci tous en même temps. En utilisant des cryptogrammes qui peuvent mettre en paquet 8 192 valeurs en même temps, nous avons pu réduire le nombre de cryptogrammes à seulement 2 124. À environ 1 Mo par cryptogramme, cela fait en sorte que l'ensemble de données chiffrées représente environ deux gigaoctets (Go). Comme les données en texte clair prennent 84 mégaoctets (Mo), cela a abouti à un facteur d'élargissement d'environ 25 fois. En tout, le traitement informatique chiffré a pris environ 19 minutes, ce qui est 30 fois plus long que le traitement informatique non chiffré.
Application 2 : Classification de texte confidentiel fondée sur le chiffrement homomorphe
Ensuite, nous avons attaqué la tâche d'entraînement pour l'apprentissage automatique. L'entraînement pour l'apprentissage automatique est une tâche réputée pour être coûteuse, donc nous ne savions pas exactement si nous serions capables de mettre en œuvre une solution pratique.
Souvenez‑vous de la première tâche dans le flux de travail des données de lecteurs optiques – les descriptions de produits pleines de bruit qui dépendant du détaillant doivent être classées par code du SCPAN. C'est une tâche de classification de textes comprenant de multiples catégories. Nous avons créé un ensemble de données synthétique à partir d'un répertoire en ligne de descriptions de produits et nous leur avons attribué un de cinq codes du SCPAN.
L'exécution d'un réseau neuronal représente essentiellement la multiplication d'un vecteur par une série de matrices, et l'entraînement d'un réseau neuronal demande des passages vers l'avant, ce qui consiste à évaluer les données d'entraînement dans le réseau, ainsi que des passages vers l'arrière, qui utilisent la descente de gradient (stochastique) et la règle de chaînage afin de trouver la meilleure façon de mettre à jour les paramètres du modèle pour améliorer la performance. Tout cela se résume à la multiplication de valeurs par d'autres valeurs, et en ayant accès à la multiplication homomorphe, l'entraînement d'un réseau chiffré est possible en théorie. En pratique, cela est entravé par une limite de base du procédé CKKS : la nature échelonnée des multiplications homomorphes. Nous discuterons d'abord de cet élément, puis nous étudierons les différents aspects du protocole désignés pour l'atténuer.
Niveaux des cryptogrammes dans CKKS
Afin de protéger vos données pendant le chiffrement, le procédé CKKS ajoute un peu de bruit à chaque cryptogramme. L'inconvénient est que ce bruit s'accumule avec les opérations consécutives et doit être modulé. Le CKKS a un mécanisme intégré pour cela, mais malheureusement il ne permet qu'un nombre limité d'opérations sur un même cryptogramme.
Supposons que nous avons deux cryptogrammes fraîchement chiffrés : et . Nous pouvons les multiplier de manière homomorphe pour obtenir le cryptogramme . Le problème est que le bruitNote de bas de page 5 dans le cryptogramme qui en résulte est beaucoup plus important que pour ceux nouvellement chiffrés, donc si nous le multiplions par le cryptogramme fraîchement chiffré , le résultat serait touché par cette discordance.
Il faudrait d'abord remettre à l'échelle le cryptogramme . C'est géré de façon transparente par la bibliothèque de CH, mais sous le capot, le cryptogramme est déplacé dans un espace légèrement différent. Nous disons que a descendu d'un niveau, ce qui signifie que le cryptogramme a commencé au niveau , et après la remise à l'échelle, il se trouve sur le niveau . La valeur est déterminée par les paramètres de sécurité que nous choisissons lorsque nous configurons le procédé de CH.
Nous avons maintenant qui a une quantité normale de bruit, mais qui se trouve au niveau , et le fraîchement chiffré qui est toujours au niveau . Malheureusement, nous ne pouvons pas effectuer d'opérations sur les cryptogrammes qui se trouvent sur différents niveaux, donc nous devons d'abord réduire le niveau de à par permutation modulée. Maintenant que les deux cryptogrammes sont au même niveau, nous pouvons enfin les multiplier comme souhaité. Il n'est pas nécessaire de remettre à l'échelle de résultat des additions, mais nous devons le faire pour chaque multiplication.

Figure 4 : Une illustration des niveaux.
Une illustration des niveaux. À gauche nous pouvons voir le niveau sur lequel chaque cryptogramme se trouve : de haut en bas, nous avons les niveaux , et . Les valeurs nouvellement chiffrées , et se trouvent toutes au niveau tout en haut. Après la multiplication, descend au niveau . Si nous voulons multiplier par , nous devons d'abord descendre au niveau . Le produit qui en résulte, , se trouve au niveau .
Cette histoire de niveaux a deux conséquences. Premièrement, le développeur doit être conscient du niveau des cryptogrammes qu'il utilise. Deuxièmement, les cryptogrammes atteindront éventuellement le niveau 0 après de nombreuses multiplications consécutives; à ce moment‑là, ils sont épuisés et nous ne pouvons plus effectuer d'autres multiplications.
Il y a quelques options pour élargir les calculs au‑delà du nombre de niveaux disponibles. La première est un processus qui s'appelle le bootstrap, selon lequel le cryptogramme est déchiffré de manière homomorphe puis chiffré de nouveau, ce qui crée un nouveau cryptogramme. Ce processus peut en théorie permettre un nombre illimité de multiplications. Cependant, cette charge supplémentaire ajoute un coût au traitement informatique. Il est également possible d'actualiser les cryptogrammes en les renvoyant au détenteur de clé secrète, qui peut les déchiffrer et les chiffrer de nouveau avant de les renvoyer sur le nuage. Le va‑et‑vient des cryptogrammes ajoute un coût en communication, mais ça en vaut parfois la peine lorsqu'il n'y a pas beaucoup de cryptogrammes à envoyer.
Incidence des niveaux sur notre structure de réseau
Nous devions envisager cette contrainte fondamentale relative au CH lorsque nous avons conçu notre réseau neuronal. Le processus d'entraînement d'un réseau demande de réaliser une prédiction, d'évaluer la prédiction et de mettre à jour les paramètres du modèle. Cela signifie que chaque tour, ou époque, d'entraînement consomme des niveaux multiplicatifs. Nous avons essayé de réduire au minimum le nombre de multiplications nécessaires pour traverser le réseau d'un bout à l'autre afin de maximiser le nombre de tours d'entraînement disponibles. Nous décrirons maintenant la structure du réseau et la stratégie d'encodage.
L'architecture du réseau a été inspirée par la solution existante pour la production. Cela correspondait à un modèle d'ensemble d'apprenants linéaires. Nous avons entraîné plusieurs réseaux à couche simple et, au moment de la prédiction, nous avons fait en sorte que chaque apprenant vote pour chaque entrée. Nous avons choisi cette approche parce qu'elle réduisait la quantité de travail requis pour entraîner chaque modèle – moins de temps d'entraînement signifiait moins de multiplications.
Chaque couche dans un réseau neuronal est une matrice des poids des paramètres multipliée par des vecteurs de données pendant le passage vers l'avant. Nous pouvons adapter cela au CH en chiffrant chaque vecteur d'entrée en un seul cryptogramme et en chiffrant chaque rang de la matrice des poids en un autre cryptogramme. Le passage vers l'avant devient alors plusieurs multiplications vectorielles, suivies de nombreuses rotations et multiplications logarithmiques pour calculer la somme des extrants (souvenez‑vous que la multiplication matricielle est une série de produits scalaires, qui constitue une multiplication des composantes suivie d'un calcul de la somme des valeurs qui en résultent).
Le prétraitement est une partie importante de toute tâche de classification de texte. Nos données étaient constituées de courtes phrases, qui comportaient souvent des acronymes ou des abréviations. Nous avons choisi un encodage à caractère -gramme, où égale trois, quatre, cinq et six – « crème glacée » a été divisé en 3 grammes {« crè », « rèm », « ème », « vglav », « vlac », « vacé », « céev »}. Ces -grammes ont été recueillis et dénombrés pour l'intégralité de l'ensemble de données et ont été utilisés pour chiffrer à chaud chaque entrée. Un vectoriseur de hachageNote de bas de page 6 a été utilisé pour réduire la dimension des entrées chiffrées.
De la même façon que nous avons mis en paquet de multiples listes dans l'analyse statistique, nous avons constaté que nous pouvions mettre en paquet de multiples paquets et les entraîner en même temps. L'utilisation d'une valeur signifiait que nous pouvions mettre en paquet 16 384 valeurs dans chaque cryptogramme, donc si nous hachions nos données en 4 096 dimensions, nous pourrions mettre quatre modèles dans chaque cryptogramme. Cela avait l'avantage supplémentaire de réduire le nombre de cryptogrammes requis pour chiffrer notre ensemble de données par un facteur de quatre. Cela signifie que nous pouvions entraîner quatre modèles simultanément.
Notre choix de paramètres de chiffrement signifiait que nous avions entre 12 et 16 multiplications avant de manquer de niveaux. À partir d'un réseau à une seule couche, le passage vers l'avant et le passage vers l'arrière nécessitaient chacun deux multiplications, ce qui nous laissait de la place pour trois à quatre époques avant que nos cryptogrammes modèles soient épuisés. Nos ensembles signifiaient que nous pouvions entraîner des modèles valant plusieurs cryptogrammes si désirés, ce qui signifie que nous pourrions avoir autant d'apprenants que souhaité au coût de temps supplémentaire d'entraînement. En modulant soigneusement quel modèle a appris au sujet de quelles données, cela nous a aidés à maximiser la performance globale de l'ensemble.
Notre ensemble de données représentait 40 000 exemples d'entraînements et 10 000 exemples de test qui ont tous été distribués également dans nos cinq classes. Entraîner quatre sous‑modèles en six époques a pris cinq heures et a permis d'obtenir un modèle qui a obtenu une précision de 74 % sur l'ensemble des essais. En utilisant la tactique d'actualisation des cryptogrammes précédemment décrite, nous pouvons hypothétiquement entraîner pendant autant d'époques que nous le voulons, bien que chaque actualisation ajoute des coûts de communication supplémentaires au processus.Note de bas de page 7 Après l'entraînement, le nuage renvoie le modèle chiffré à StatCan, et nous pouvons l'exécuter en texte clair sur les données en production. Ou nous pouvons conserver le modèle chiffré sur le nuage et exécuter une inférence de modèle chiffrée lorsque nous avons de nouvelles données à classer.
Conclusion
Cela conclut la série de Statistique Canada sur les applications CH pour les données de lecteurs optiques examinées à ce jour. Le CH a un certain nombre d'autres applications qui pourraient s'avérer intéressantes pour un organisme national de statistique comme l'intersection d'ensembles confidentiels, selon laquelle deux parties ou plus calculent ensemble l'intersection d'ensembles de données confidentielles sans les partager, ainsi que le couplage d'enregistrements préservant la confidentialité, selon lequel les parties effectuent des couplages, des partages et des traitements informatiques sur des microdonnées jointes à leurs ensembles de données confidentielles.
Il y a encore beaucoup de choses à explorer dans le domaine des TAC et StatCan travaille à tirer profit de ce nouveau domaine pour protéger les renseignements personnels des Canadiens tout en fournissant des renseignements de qualité qui compte.
Rencontre avec le scientifique des données

Si vous avez des questions à propos de mon article ou si vous souhaitez en discuter davantage, je vous invite à une Rencontre avec le scientifique des données, un événement au cours duquel les auteurs rencontrent les lecteurs, présentent leur sujet et discutent de leurs résultats.
Jeudi, le 15 décembre
14 h 00 à 15 h 00 HE
MS Teams – le lien sera fourni aux participants par courriel
Inscrivez-vous à la présentation Rencontre avec le scientifique des données. À bientôt !
Bibliographie
Système de classification des produits de l'Amérique du Nord (SCPAN), Canada 2017, version 1.0
Cheon, J. H., Kim, A., Kim, M., et Song, Y. (2016). Homomorphic Encryption for Arithmetic of Approximate Numbers.(en anglais seulement). Cryptology ePrint Archive.
Gentry, C. (2009). A fully homomorphic encryption scheme. Thèse de doctorat, Stanford University. Craig Gentry's PhD Thesis (en anglais seulement)
Zanussi, Z., Santos B., et Molladavoudi S. (2021). Supervised Text Classification with Leveled Homomorphic Encryption. Dans Proceedings 63rd ISI World Statistics Congress (Vol. 11, p. 16). International Statistical Institute - Statistical Science for a Better World (en anglais seulement)
- Date de modification :